ABC386 振り返り | tunamaguro's blog

はじめに

2024/12/28に開催されたABC386の振り返りです。今回はA~Cの三冠で終了しました。終了後Fまで解説を確認しながら解いたので、それも併せて記載します

A - Full House 2

https://atcoder.jp/contests/abc386/tasks/abc386_a

入力がスリーカードか2ペアかを判定すればよいです。ただし、スリーカードのとき4枚目も同じだと、フルハウスを達成できないので、それを合わせて判定する必要があります

fn main() {
    input! {a:i32,b:i32,c:i32,d:i32}
    let mut arr = [a, b, c, d];
    arr.sort();

    let have_three =
        (arr[0] == arr[1] && arr[1] == arr[2]) || (arr[1] == arr[2] && arr[2] == arr[3]);

    let have_double_two = (arr[0] == arr[1]) && arr[2] == arr[3];

    let all_same = arr[0] == arr[1] && arr[1] == arr[2] && arr[2] == arr[3];

    if !all_same && (have_three || have_double_two) {
        println!("Yes")
    } else {
        println!("No")
    }
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61148555

B - Calculator

https://atcoder.jp/contests/abc386/tasks/abc386_b

基本的に1文字ずつ読み進め、0が連続するときのみ2文字進めるようにします

fn main() {
    input! {s:Chars}
    let mut i = 0;
    let mut ans = 0;
    while s.len() > i {
        if s.len() - 1 == i {
            ans += 1;
            break;
        }

        if s[i] == '0' && s[i + 1] == '0' {
            ans += 1;
            i += 2;
        } else {
            ans += 1;
            i += 1;
        }
    }

    println!("{}", ans)
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61152408

C - Operate 1

https://atcoder.jp/contests/abc386/tasks/abc386_c

$|S| == |T|$ の時とそうでないときで分岐させました。長さが等しいときは単純に異なる文字が $K$ 文字以下か判定、長さが異なるときはインデックスをずらしながら同じ文字かどうかを判定しています。

fn main() {
    input! {k:usize,s:Chars,t:Chars}
    if s.len() == t.len() {
        let mut diffs = 0;
        for (si, ti) in s.iter().zip(t.iter()) {
            if si != ti {
                diffs += 1;
            }
        }

        if diffs <= k {
            println!("Yes");
        } else {
            println!("No")
        }
    } else {
        let mut sidx = 0;
        let mut tidx = 0;
        let s_is_longer = s.len() > t.len();

        let mut diffs = 0;
        while s.len() > sidx && t.len() > tidx {
            if s[sidx] != t[tidx] {
                diffs += 1;
                if s_is_longer {
                    sidx += 1;
                } else {
                    tidx += 1
                }
            }

            sidx += 1;
            tidx += 1;
        }

        let len_diff = s.len().max(t.len()) - s.len().min(t.len());

        if diffs <= k && len_diff <= k {
            println!("Yes")
        } else {
            println!("No")
        }
    }
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61166737

振り返りでの気づき

これを書きながら問題が2つあることに気づきました。長さが異なるとき分岐は以下のようになっています

while s.len() > sidx && t.len() > tidx {
    if s[sidx] != t[tidx] {
        diffs += 1;
        if s_is_longer {
            sidx += 1;
        } else {
            tidx += 1
        }
    }

    sidx += 1;
    tidx += 1;
}

本来は文字が異なるとき、長いほうのインデックスだけを進める必要があります（それを意図していました）が、ループの終わりで無条件に進めているためそうなっていません。そのため、backとblackのようなケースで次のように処理され、たまたま正しいですが1文字処理できていません

1回目bとbで等しいため、sidx = 1,tidx = 1になる
2回目aとlで等しくなく、s_is_longer = falseなのでtidxが1つ多く進められ、sidx = 2, tidx = 3になる
3回目cとcが比較されるが、本当はback2文字目のaとblack3文字目のaが比較されるべき（black3文字目のaを読み飛ばしている）

また、ループ終了時にそれぞれのインデックスが最後まで進んでいるか検証していないので、それで正しく判定できないことがありそうです

これらの問題を修正するとこのようになり、これでもACできました

fn main() {
    input! {k:usize,s:Chars,t:Chars}
    if s.len() == t.len() {
        let mut diffs = 0;
        for (si, ti) in s.iter().zip(t.iter()) {
            if si != ti {
                diffs += 1;
            }
        }

        if diffs <= k {
            println!("Yes");
        } else {
            println!("No")
        }
    } else {
        let mut sidx = 0;
        let mut tidx = 0;
        let s_is_longer = s.len() > t.len();

        let mut diffs = 0;
        while s.len() > sidx && t.len() > tidx {
            if s[sidx] != t[tidx] {
                diffs += 1;
                if s_is_longer {
                    sidx += 1;
                } else {
                    tidx += 1
                }
            } else {
                sidx += 1;
                tidx += 1;
            }
        }

        let slen = s.len();
        let tlen = t.len();
        if sidx != slen || tidx != tlen {
            diffs += (slen - sidx).max(tlen - tidx);
        }

        if diffs <= k {
            println!("Yes")
        } else {
            println!("No")
        }
    }
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61255442

D - Diagonal Separation

https://atcoder.jp/contests/abc386/tasks/abc386_d

これ以降の問題は解けなかったので、解説を見たうえでの理解です

条件からマス $(x,y)$ が黒のとき、左上がすべて黒である必要があります。それが満たされていれば条件を満たすように塗り分けることができます。すべてのマスについて精査すると、 $M^2$ の計算量がかかりますが、今回は最大で $M = 2 \times 10^5$ なので間に合いません。

そこで塗られているマスをX,Yの順にソートすることで、Yの最小値のみを管理すれば良いようになります。ソート後の並び順は次のようになります

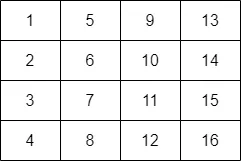
ソート後の並び順

そのため、白で塗られたマスの最小のYを更新しながら、それより大きな黒マスが見つかった時点で条件を満たせなくなることがわかります。これはX,Yの順にソートされているため、Yが大きいマスが持つ黒を配置できないエリアが、Yが小さいマスの持つエリアに包含されているためです

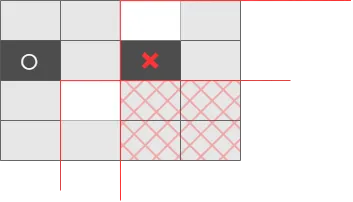
包含されている

最終的な解くプログラムは次のようになります

fn main() {
    input! {_n:usize,m:usize,colors:[(i32,i32,char);m]}

    let colors = colors.into_iter().sorted().collect::<Vec<_>>();

    let mut min_y = i32::MAX;
    for (_x, y, c) in colors {
        if c == 'W' {
            min_y = min_y.min(y);
        } else if y >= min_y {
            println!("No");
            return;
        }
    }
    println!("Yes")
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61206886

反省

解説に記載のあるマス $(x,y)$ が黒のとき、左上がすべて黒である必要があることに気づけていませんでした。単純に $x_i < x, y_i < y$ が黒になると思っていたため、入力例すら突破できずに悩んでいたところ、終了時刻になっていました。実際に条件に合うように自分で作図していれば、正しく認識できていただろうと反省しています

E - Maximize XOR

https://atcoder.jp/contests/abc386/tasks/abc386_e

条件から部分列の組み合わせの数が $10^6$ 個以下であることが保証されているため、すべての選び方を処理しても理論的には十分間に合います。しかし、再帰のやり方によって「要素を選ぶ」「要素を選ばない」の分岐が毎回発生するため、 $K$ が大きいとき再帰の回数は非常に大きな数になり間に合いません。

def func(x: list[int], i: int):
    # x = 選んだ要素のインデックス一覧
    if len(x) == K:
        # K 個選んだので処理
        return
    if i == N:
        return
    # i番目を「選ぶ」場合
    func(x + [i], i + 1)
    # i番目を「選ばない」場合
    func(x, i + 1)

そこで、XORの同じ数で演算すると元に戻る次の性質を利用します

a \oplus b = c \newline c \oplus b = a

$K$ と $N-K$ のどちらか小さいほうだけを処理することで、最悪の計算量を抑えることができます。 $K$ のほうは愚直に計算するだけですが、 $N-K$ のほうを処理する場合は、先にすべてのXORを計算しそこから再度XORを取ることで、（上記の性質から）答えが出てきます

fn func(a: &[usize], idx: usize, c: usize, current_xor: usize, ans: &mut usize) {
    // c = 0(残り選択数が 0) ならば、最大値を更新して戻る
    if c == 0 {
        if current_xor > *ans {
            *ans = current_xor;
        }
        return;
    }
    // idx が配列の長さに達したら探索を終了
    if idx == a.len() {
        return;
    }
    // A[idx] を使う場合
    func(a, idx + 1, c - 1, current_xor ^ a[idx], ans);
    // A[idx] を使わない場合
    func(a, idx + 1, c, current_xor, ans);
}

fn main() {
    input! {n:usize,k:usize,a:[usize;n]}

    let mut ans = 0;

    if k <= n - k {
        func(&a, 0, k, 0, &mut ans);
    } else {
        let mut all_xor = 0;
        for &val in &a {
            all_xor ^= val;
        }
        func(&a, 0, n - k, all_xor, &mut ans);
    }

    println!("{}", ans)
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61221157

よりRustっぽく書き直したものはこちらです

提出結果: https://atcoder.jp/contests/abc386/submissions/61221532

F - Operate K

https://atcoder.jp/contests/abc386/tasks/abc386_f

いわゆるレーベンシュタイン距離が $K$ 以下かどうかを判定する問題です。レーベンシュタイン距離を求めるプログラムはRosetta Codeなどですでに実装が公開されています。ですが、このプログラムの計算量は $O(|S||T|)$ なので、今回の制約 $|S|,|T| \leq 5 \times 10^5$ では間に合いません。またメモリも $|S| \times |T|$ byte程度使用するため、そのままではメモリが不足します

レーベンシュタイン距離を求めるアルゴリズム自体の解説は次のページがわかりやすいです
https://nw.tsuda.ac.jp/lec/EditDistance/

そこで $K$ が20以下であることに着目し、文字列の長さの差が $K$ より大きいものを無視することで、この問題を時間内に処理できます。イメージとしては次のようにずらしながら処理していく感じです。灰色部分は満たさないことが明白なので処理しません

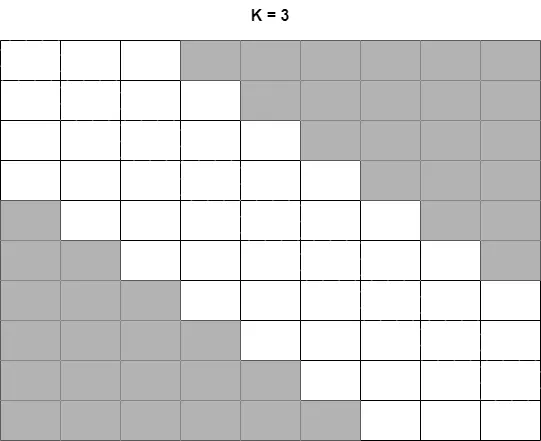
処理イメージ

最終的な実装は次のようになります。Rosetta Codeの実装とi,jの振り方が違うことに注意してください

fn main() {
    input! {k:usize,s:Chars,t:Chars}

    if (s.len() as i32 - t.len() as i32).abs() > k as i32 {
        println!("No");
        return;
    }

    let s_length = s.len();
    let t_length = t.len();

    let mut dp = vec![vec![usize::MAX; 2 * k + 1]; s_length + 1];

    dp[0][k] = 0;

    for i in 0..=s.len() {
        for dj in 0..=(2 * k) {
            let j = i as i32 + dj as i32 - k as i32;
            if j < 0 {
                continue;
            }
            let j = j as usize;
            if j > t_length {
                break;
            }

            if i > 0 && dj < 2 * k {
                dp[i][dj] = dp[i][dj].min(dp[i - 1][dj + 1] + 1)
            }
            if j > 0 && dj > 0 {
                dp[i][dj] = dp[i][dj].min(dp[i][dj - 1] + 1)
            }

            if i > 0 && j > 0 {
                let add = if s[i - 1] == t[j - 1] { 0 } else { 1 };
                dp[i][dj] = dp[i][dj].min(dp[i - 1][dj] + add)
            }
        }
    }

    if dp[s_length][k + t_length - s_length] <= k {
        println!("Yes")
    } else {
        println!("No")
    }
}

提出結果: https://atcoder.jp/contests/abc386/submissions/61258485

感想

Dが解けなかったのがかなり悔しいですが、XORの性質やレーベンシュタイン距離の求め方など学びの多いコンテストでした